Probability Of Straight Flush Texas Holdem
There are 41,584 straight flushes, of which 4324 are royal, out of 52C7 = 133,784,560 hands. That gives you a royal flush probability of 3.23206E-05 (or 1 in 30,940) and a straight flush (including royal) probability of 3.108281E-04 (or 1 in 3217+.) 1.2K views View 2 Upvoters. 1.10 Odds On the Flop in Texas Hold’em. 1.10.1 Outs; 1.10.2 Straight and Flush Draw Odds; 1.10.3 On the flop, when you have: 1.11 Odds of hitting a hand by the river from the flop. 1.11.1 On the flop, when you have: 1.12 All-in One-on-One in Texas Hold’em. 1.12.1 Preflop matchups when played to showdown: 1.13 Just-for-Fun Texas Hold’em odds. However, after you get used to pot odds you will just remember that things like flush draws are around 4:1 odds. To be honest, you won't even need to do this step the majority of the time, because there are very few ratios that you need to remember, so you can pick them off the top of your head and move on to step 2. 88ProBet is the preferred online betting sports and live Odds Of Making A Straight Flush In Texas Holdem casino in Singapore. We gained our popularity through the creation of numerous online casino games, guaranteed payout when you win at any of our jackpot games, sportsbook betting, live Odds Of Making A Straight Flush In Texas Holdem casino games.
To calculate the frequency of four of a kind, first note that there are 13 different ranks in which you can get four of a kind. For any given rank, the possible hands that give four of a kind in that rank all include the four cards of that rank as well as any three additional cards. There are C48,3 = 17,296 different ways of choosing these three additional cards, so we have a total of 13 · 17,296 = 224,848 different four of a kind hands. This gives a frequency of (224,848/133,784,560) = 0.0017.
To find the frequency of straight flushes, sort all straight flush hands by the high card of the highest straight flush in the hand. For ace high straight flushes in any of the four suits you need the A - K - Q - J - 10 of the given suit and then any 2 of the remaining 47 cards. This gives a total of C47,2 = 1,081 distinct hands. For straight flushes that are not ace high the same argument holds except that one of the remaining 47 cards would give you higher straight flush if it were in your hand (for example, if you have 10 - 9 - 8 - 7 - 6 in hearts, if one of your two other cards was a jack of hearts you would have a jack high straight flush). Therefore, in these cases there are only C46,2 = 1,035 distinct straight flush hands. So the total number of straight flush hands is (1,081 · 4) + (1,035 · 4 · 9) = 41,584 hands (the nine in the second parenthesis comes from the fact that there are nine different possible non-ace high cards for straights - a 2,3, or 4 high straight can not occur). The corresponding frequency is then (41,584/133,784,560) = 0.00031.

To count the number of full house hands, we divide up the types of full houses by looking at the two cards that are not used as part of the final hand. These two cards can either be a pair (but of a different rank than the triple or the pair you are using for the full house, or else you would have four of a kind), one of the two cards could be of the same rank as your pair (giving you two triples and one card of some different rank), or the two cards could be of different ranks from each other, the triple, and the pair.
- We first consider the case of the unused cards being a pair. We can choose the rank for the triple in 13 ways. Once a rank is chosen we can pick the three cards for the triple in C4,3 = 4 ways. We can then choose the two ranks for the two pairs in C12,2 = 66 ways. For each pair, once we have chosen the rank we can choose the cards for the pair in C4,2 = 6 ways. So we have a total of 13 · 4 · 66 · 62 = 123,552 full house hands of this type.
- Now we consider the case of two triples. We can choose the ranks for the triples in C13,2 = 78 ways, and for each triple we can then choose the cards for the triple in C4,3 = 4 ways. There are then 44 remaining cards from which to choose the last card of the hand, so we have a total of 78 · 42 · 44 = 54,912 hands of this type.
- Finally we consider the case of two cards of different rank from each other, the triple, and the pair. As above, the cards for the triple can be chosen in 13 · C4,3 = 52 ways and the cards for the pair can then be chosen in 12 · C4,2 = 72 ways. We can choose the two ranks for the remaining two cards in C11,2 = 55 ways, and for each rank we can choose any of the four cards of that rank. This gives a total of 52 · 72 · 55 · 42 = 3,294,720 hands of this type.
Therefore, we have a total of 3,473,184 full house hands. This gives a frequency of (3,473,184/133,784,560) = 0.02696.
For additional calculations, as well as the frequencies for 5-card poker hands (which tend to be significantly easier to calculate), see for example Wikipedia.
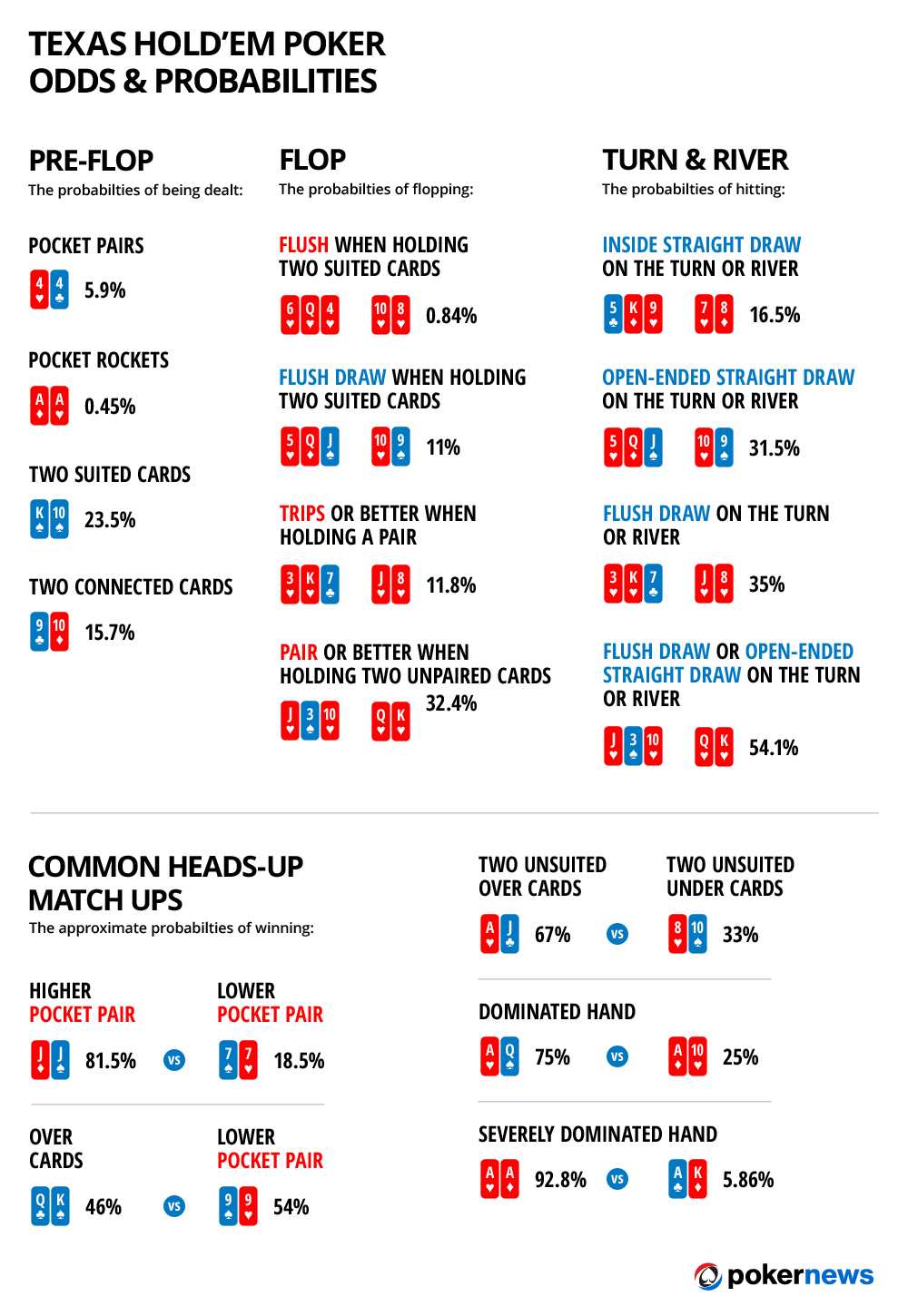
Our common flop odds chart shows the exact odds of flopping specific hand or draw types with various hole card groupings in Texas Holdem.
Remember that every mistake you make preflop will only be magnified on later streets. The chart below clearly shows that playing weak hole cards (for example three gapped connectors) will rarely give you the best hand on the flop.
This is why you should play only a narrow range of the best hole cards and fold everything else. It is especially important when you are a beginner. The more weak hands you play, the more money you will lose in the long term.
Common flop odds chart
| Hole Cards | Flopping | Odds |
| Unpaired Hole Cards | exactly one pair by pairing a hole card | 26.939% |
| exactly two pair by pairing a hole card and pairing on the board | 2.02% | |
| exactly two pair by pairing each of your hole cards | 2.02% | |
| exactly trips by flopping two cards to a hole card | 1.347% | |
| exactly a full house, trips of one hole card and pairing the other | 0.092% | |
| exactly four of a kind, three cards to one of your hole cards | 0.01% | |
| Paired Hole Cards | exactly two pair by pairing the board | 16.163% |
| exactly trips by flopping a set for your pocket pair | 10.775% | |
| exactly a full house, a set to your hole pair and pairing the board | 0.735% | |
| exactly a full house, by the board tripping up | 0.245% | |
| exactly four of a kind, two cards to your hole pair | 0.245% | |
| Two Unsuited Cards | a flush draw | 2.245% |
| Two Suited Cards | a flush (including straight flush) | 0.842% |
| a flush draw | 10.944% | |
| Connectors (54 to JT) | a straight (including straight flush) | 1.306% |
| an 8 out straight draw (excluding gutshots) | 10.449% | |
| One Gapped Connectors (53 to QT) | a straight (including straight flush) | 0.98% |
| an 8 out straight draw (excluding gutshots) | 8.08% | |
| Two Gapped Connectors (52 to KT) | a straight (including straight flush) | 0.653% |
| an 8 out straight draw (excluding gutshots) | 5.224% | |
| Three Gapped Connectors (A5 to AT) | a straight (including straight flush) | 0.327% |
| an 8 out straight draw (excluding gutshots) | 2.612% |
More articles on poker probability:
Probability Of Straight Flush Texas Holdem Rules
Poker odds calculator
Poker outs and odds
Pot odds and expected value
Sklansky bucks
Implied odds
Reverse implied odds
Poker hand probability chart
Common flop odds chart
Pocket pairs - flopping overcards odds
Probability Of Straight Flush Texas Holdem Odds
Go back to the Online Poker Strategy.